鲁晨光中文主页 English Homapage Papers on ArXiv Recent papers about Semantic Information and Statistical Learning
2025年4月于英文Open期刊Entropy发表英文综述文章 ：《香农信息论的语义推广（G理论）和应用》
Entropy 是MDPI出版公司出版的一个专业期刊，汇集了全球许多对熵和信息感兴趣的作者和读者。这篇是我在Entropy上面发表的第5篇文章。
下面是中英文版。
|
中文综述文章:
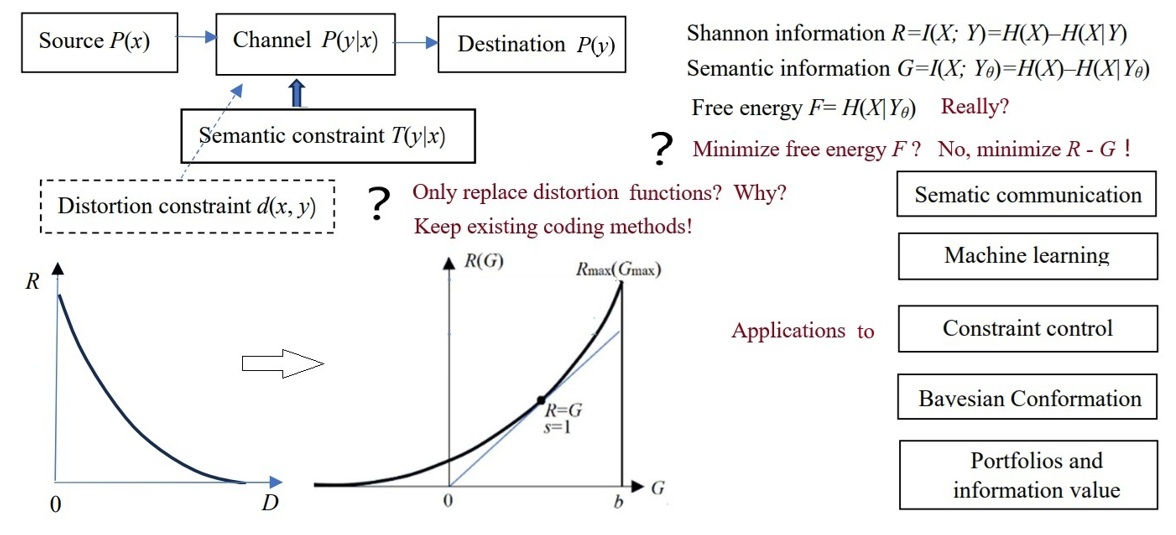
摘要:语义通信是否需要一个和香农信息论平行的语义信息论，还是只需要在香农信息论基础上推广？作者主张后者。语义信息G理论就是一个推广香农信息论得到的语义信息论。推广的方法是：仅仅添加语义信道，它由一组真值或隶属函数构成。通过真值函数可以定义语义失真，语义信息量和语义信息损失。语义信息量就等于Carnap和Bar-Hillel的语义信息量减去失真量， 最大语义信息准则等价于最大似然准则，类似于正则化最小误差平方准则。本文显示了G理论用于语义的和电子的语义通信，机器学习，约束控制，贝叶斯确证，投资组合和信息价值。改进机器学习方法涉及多标签学习和分类、最大互信息分为类，混合模型，求解隐含变量。文中还通过统计物理学分析，得到有意义结论：香农信息就相当于自由能，语义信息就相当于局域平衡系统的自由能和做功能力；最大信息效率就相当于用自由能做功时的最大热功效率；Friston的最小自由能原理可以改进为更加易于理解和使用的最大信息效率原理。文中联系投资组合理论讨论了信息价值。文中比较了G理论和其他语义信息理论的区别和联系，讨论了它表示复杂数据语义的局限性。
关键词： 语义信息论，语义信息测度，信息率失真，信息率逼真，变分贝叶斯，最小自由能，最大信息效率，投资组合，信息价值，约束控制. 。
|
English
Review:
A
Semantic Generalization of Shannon's Information Theory and Applications Abstract: A new trend in deep learning, represented by Mutual Information Neural Estimation (MINE) and Information Noise Contrast Estimation (InfoNCE), is emerging. In this trend, similarity functions and Estimated Mutual Information (EMI) are used as learning and objective functions. Coincidentally, EMI is essentially the same as Semantic Mutual Information (SeMI) proposed by the author 30 years ago. This paper first reviews the evolutionary histories of semantic information measures and learning functions. Then, it briefly introduces the author’s semantic information G theory with the rate-fidelity function R(G) (G denotes SeMI, and R(G) extends R(D)) and its applications to multi-label learning, the maximum Mutual Information (MI) classification, and mixture models. Then it discusses how we should understand the relationship between SeMI and Shannon’s MI, two generalized entropies (fuzzy entropy and coverage entropy), Autoencoders, Gibbs distributions, and partition functions from the perspective of the R(G) function or the G theory. An important conclusion is that mixture models and Restricted Boltzmann Machines converge because SeMI is maximized, and Shannon’s MI is minimized, making information efficiency G/R close to 1. A potential opportunity is to simplify deep learning by using Gaussian channel mixture models for pre-training deep neural networks’ latent layers without considering gradients. It also discusses how the SeMI measure is used as the reward function (reflecting purposiveness) for reinforcement learning. The G theory helps interpret deep learning but is far from enough. Combining semantic information theory and deep learning will accelerate their development. Keywords: semantic information theory; semantic information measure; information rate-distortion; information rate-fidelity; variational Bayes; free energy principle; maximum information efficiency; portfolio; information value; constraint control |
Graphical摘要：
