(27.5) ” (1)朱顶余 何沛平 著
2003，12，公布于熵信息复杂性网站
第四章 处于重力场中的平衡态体系内
存在着稳恒的温度梯度
三.用“相对论热力学关系式”导出温度梯度关系式
本文对《统计物理学》中“力场中热力学系统的第一平衡条件”进行讨论,确认经典热力学原理描述的平衡态体系中各点的温度等于常数的说法具有局限性。得到“力场中的绝热平静的体系中存在着永恒的温度梯度, 无传导热流伴随 ”的结论。
1 引 言
人们总是不肯相信力场可导致流体中存在着稳恒的温度梯度, 当然也就不易发现力场对热力学规律尤其是热流规律的重要影响, 其实相对论热力学已确认引力可导致温度梯度, 但这往往不被人们理解和注意, 导致人们对一些热学自然现象产生不切实际的理解,本文试图就此展开讨论。
2 两种描述的比较
我们将由相对论方法给出的力场中“平衡态”体系的温度分布规律与由经典热力学方法所给出的温度分布规律进行比较。
在《统计物理学》[1]教材中,§27. “相对论范围内的热力学关系式”一节指出“第一平衡条件” 为
“T=常数
(27.5) ” (1)
“当平衡时,
在物体中｜
｜越大的地方,
即在物体中越深的地方,
温度就越高。当过渡到非相对论力学的极限情形时(c→∞),(27.5)
变为T=常数, 这正是所预期的。 ”
(1)式中T为温度,
为引力势,c为真空中的光速。 由(1)
式分析可知,
经典热力学描述的平衡态体系中各点的温度仍然应等于常数,此乃属留有余地的近似说法,
因为光速是有限的确定值(有
μ。为真空磁导率常数,
ε。
为真空介电常数。且有?/FONT>光速不变原理?而实际上并非无穷大。
而在《流体力学》 教材中指出的绝热稳定流能量方程为
常数,
(2)
(2) 式中,H°为单位质量的焓(比焓),v为流体的速度,(1/2)v2为单位流质所拥有的动能(比动能),g为引力加速度(常数),h为参考高度,gh为匀强力场的势函数(比势能) 。
当流体作匀速直线流动或准静态转移时,(2) 式变为
常数,
(3)
对于理想气体有
,
(4)
其中,
为流体的等压比热常数(cP/m) 。故(3) 式可改写成
常数,
或
常数, (5)
对于匀强力场,(1)
式中的引力势=gh, 令(1) 式中常数为C ,故(1)
式可表示成
,
(6)
对比(5) 、(6)
式可知,(1) 式中的常数C与
及c2有下列关系
,
(7)
这是理所当然的,
因为光速c为常数, 
为理想气体的比热常数。
故(1)式可表为
,或
,
对于匀强力场则为
,
(8)
(8) 可写成 常数,
(9)
(9)
式是从广义相对论(引力理论) 导出的, 而(5)
式则是由工程热力学导出的, 两者居然殊途同归,
这绝不是一种巧合, 而是正确思路必然表现为互佐互通,
其结果必然是互洽的,
即对同一事实的正确描述与其使用哪种理论方法无关,
其结果必然一致。(5) 、(9)
式一致表明在匀强力场中理想气体系统的第一平衡条件是常数,
即力场中的绝热体系内各点的温度T是其参考高度h的线性函变量,
而不是与其高度无关的常数,
只有在无力场空间或同一等势面各点温度才保持同一常数。
事实上(9) 式也可仿《统计物理学》[1]教材中,§27. “相对论范围内的热力学关系式”一节中, 将“第二平衡条件” 由相对论表述过渡为经典表述的做法, 即引入mc2 的方法
(10)
其中因c→∞,
而有
故被略去了, 尤其有
的运算值得仿效,
故我们完全有理由照例将本文的(1) 式中的常数引入mc2,
即令常数为
[cP为单个粒子等压热容常数(对于理想气体),m为单个粒子的质量常数],
这在对(1) 式变形过程同样遇到的运算, 而
这就同样获得与(9)
式一样的表达式。
参考文献
[1] 朗道·栗弗席兹(前苏联) 著 杨训恺等译 1964统计物理学(人民教育出版社) P96
( Landau,L、D、and Lifshitz E、M、,Statistical Physics,Pergamon Press,1958,)
四.关于“重力场导致绝热体系内稳恒
温度梯度”的实验报告
1 实验目的
用实验验证, 一个处于重力场中的绝热系统内稳定后(平衡态), 在等势面上温度处处相等; 而在铅直方向上存在着稳恒的温度梯度, 即沿铅直方向上升而递减。
2 实验方法
用液体(水银) 温度计直接测出水银柱(与外界绝热) 两端的温度, 方案一: 水银柱水平放置; 方案二: 水银柱铅直放置(A端在上、B端在下); 方案三: 水银柱铅直放置(B端在上、A端在下) 。每种方案至少放置10小时后观测, 且在每天选中午12点和晚上21点左右分别观测两次。另外, 室温的变化会影响实验装置内的水银温度, 因此在装置上下两端外部也各放置一根温度计观测, 以便在实验数据处理时扣除这些因素。
3 实验器材
1、空心玻璃管一根, 长度1700mm, 外径8mm, 内径3mm。2、硅胶管二根, 每根长度100mm, 内径小于8mm(保证套在玻璃管上密合), 外径约10mm。3、水银约200g。4、水银温度计4根, 外径8mm, 量度范围在0℃～50℃之间, 最小刻度0.1℃, 注意在同一环境中,4根温度计的温度指示要基本一致。4、支架木板材料适当。5、保温材料适当, 分别为发泡塑料, 即常见的商品包装材料, 以及铝箔。
4 实验装置构造
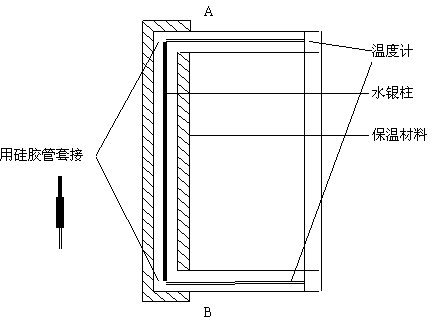
实验装置说明:
1、 水银柱夹在两片木板之间, 板的相应位置有凹槽。
2、 温度计固定在单片木板的凹槽内, 在凹槽内垫上白纸便于观测清楚。
3、 硅胶管连接着温度计和玻璃管, 胶管两端用细铜丝轧紧, 在胶管外用布条缠紧, 以便承受较大的压力。
4、 温度计的前端水银包要确保全部浸泡在胶管的水银中, 如有气泡将会影响实验的准确性, 这需反复5、 检查调试。
6、 在发泡塑料外围裹一层铝箔, 防止热辐射的影响。
7、 室内要密封, 尽可能不受外界气温变化的影响。
5 实验数据：(℃)
日期 |
时间 | 上端温度 | 下端温度 | 下上端温度差值 |
|
11.14 |
11.30 | A13.25 | B13.90 | 0.65 |
|
11.15 |
12.30 | A12.45 | B13.25 | 0.80 |
|
11.15 |
21.20 | A12.75 | B13.40 | 0.65 |
|
11.16 |
13.00 | A12.00 | B12.60 | 0.60 |
|
11.16 |
20.20 | A13.20 | B13.25 | 0.05 |
|
11.17 |
21.15 | B12.00 | A12.85 | 0.85 |
|
11.18 |
11.30 | B10.10 | A11.35 | 1.25 |
|
11.18 |
20.45 | B10.10 | A11.15 | 1.05 |
|
11.19 |
11.30 | B9.85 | A10.85 | 1.00 |
|
11.19 |
22.00 | B10.85 | A11.40 | 0.55 |
实验装置水平放置稳定后两端温度会趋于温度一致, 这种情况数据略。本实验的几天内为非晴天,室内温度在10.00℃～13.00℃之间, 每天室温变化幅度、速度很小, 对实验影响较小。本实验中的温度计最小刻度为0.10℃, 数据中出现的0.05℃为估读值。另外观测表明在装置的下端室温比上端室温平均高0.10℃。
实验装置上下倒置观测(取平均值) 可抵消实验装置不对称等因素带来的干扰。
6 实验数据处理和结论
本实验数据剔除一个最高值1.25℃及一个最低值0.05℃, 其它数据取算术平均值, 再减去0.10℃, 即得下端高于上端温度平均差值:
本实验表明: 水银柱竖直起来后, 很短时间即可表现出下端温度升高, 而上端温度降低, 随时间延长(历经弛豫时间)其温差值不断增加直至稳定, 且总是水银柱下端温度高于上端温度, 无一例外。
本实验原则上达到了预期目的, 至少能够定性证明一个处于重力场中的绝热系统稳定后, 在等势面上温度处处相等; 而在铅直方向上存在着稳恒的温度梯度。进而初步确认经典的平衡态(均温) 原理及其相关的热学定律仅适用于等势面上, 而在非等势面上是不适用的。
实验时间:2002年11.13～11.20 ,实验地点: 江苏省涟水县县城安东路6号 (何沛平住所)
五.对重力场导致温度梯度的直观理解
1 试运用经典的分子运动论的思想方法作些尝试.
由温度梯度关系式计算可知, 地面上100米高的绝热空气柱其下端温度比上端高0.97k(这常落在实验误差范围内, 故不易被人们察觉), 而且是永恒的，这里揭示了气象学中“多方(元)大气”模型的引力基础。重力场中温度梯度关系式这个结论的推导比较抽象, 不便于理解。为了寻求较直观的理解思路, 下面试运用经典的分子运动论的思想方法作些尝试。
为了简便,现只考察力场中单原子理想气体(或稀薄气体)体系, 这时单原子
理想气体分子的热运动就象完全弹性小球在力场中作紊乱飞舞碰撞。若追踪某个
粒子观察，当其沿着场力方向运动时总是动能增加,而逆着场力方向运动总是动能减少。若对某个粒子作统计考察, 当其多次(如1023次) 掠过同一等势面时所拥有的即时速率值虽各次互不相同(由频繁的碰撞所致, 这满足麦克斯韦速率分布) ，但其统计平均值却是稳定的。当然其掠过低势等势面时的动能平均值总高于掠过高势等势面时的动能平均值，而温度是大量分子平均运动的标度，故在宏观上必然表现为气体低势层温度高于高势层温度的稳定的分布状态，这就是力场中流体内热运动能梯度分布的共同机理。
2 与喷射过程的比较
这是与喷射过程进行对比来说明:
“处于重力场中的绝热体系(终寂状态)内存在着稳恒的温度梯度,且不需付出耗散性代价”的认识的。
“喷射方程”为：h+(1/2)c2=常数(h比焓,c质元速度,l线位移)
喷射方程等于
,
(1)
“可压缩流体的静力学方程”为：h+gz=常数(h比焓,g重力加速度,z是参考高度)
“可压缩流体的静力学方程”等于
,
(2)
因为加速场的加速度a等效于重力场的加速度g, 所以(1)式与(2)式是等价的。而由“可压缩流体的静力学方程” 可直接导出“处于重力场中的绝热体系内存在着稳恒的温度梯度。”
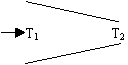
例1.一个水平放置的绝热流管,管径从左向右由粗变细,这截流管内由左向右连续地流着流体(无粘滞、可逆流动),依据喷射方程和实验事实可知,管径粗处流体速度小、压力大、密度大、温度高,管径细处流体速度大、压力小、密度小、温度低,形成稳定的温度梯度, 即T1＞T2。图示如下：
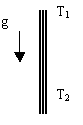
例2.一个铅直放置的绝热管内(处于重力场中),盛放着液体或固体(固体也可看着为流体,只不过流淌速度特慢而已), 笔者已通过实验证明管内也存在着稳定的温度梯度(T1＞T2)。图示如下：
例1、例2两个事实粗看起来是不相干的,其实不然,例2中存在着由上向下的重力场,而例1中存在着由右向左的加速场(等效惯性阻力场)。如果例1、例2都处在无力场空间中,则可等效认为,例1(竖直起来,左变下,右变上)等效为由下向上作加速运动,例2也等效为由下向上作加速运动。
由广义相对论的等效原理可知,重力场和加速场是等价的,本质是一致的,因此,例1、2中形成的稳定的温度梯度其机理也是一样。
请注意:例1中是可逆过程(理想化过程),不耗散,无功损耗,这才不至于产生歧义。
由上述认识立刻可知,不仅温度梯度(温度场)是热流动力,而且加速场或重力场的势梯度也是热流动力,
例2中之所以出现稳恒的温度梯度,是因为温度梯度对热流的动力方向是由下向上的,而重力场的势梯度对热流的动力方向是由上向下的,即两种不平衡势抵消,
处于“广义平衡态”。
六.对一个误解的剖析
有人认为重力场导致绝热体系内存在着稳恒的温度梯度,
这没有什么奇怪的, 因它可由状态方程来解释：
处于重力场中铅直放置(充满流体)的绝热管内有:
上部：P上V上=RT上, 下部：P下V下=RT下
因为V上=V下,所以(P上/ P下)=(T上/T下) → P上< P下 → T上<T下,
其实V上≠V下, 因为ρ上<ρ下
所以上述解释是不妥的！