朱顶余 何沛平 著
2003,8,公布于熵信息复杂性网站
第四章 处于重力场中的平衡态体系内
存在着稳恒的温度梯度
处于重力场中的平衡态体系内究竟有无稳恒的温度梯度?这是本课题的切入点,
如果答案是肯定的,
那势必成为热力学新的生长点,
因此,本题课具有重要的理论意义!为慎重起见,笔者分别用“均熵方程”
、“绝热稳定流能量方程” 、“相对论热力学关系式”3种方式进行论证,
以及一份验证的实验报告。另外,在第二篇文中给出了用“均熵方程”
推导“绝热稳定流能量方程” 的方案
, 在第三篇文中又给了“相对论热力学关系式” 与“绝热稳定流能量方程”
是相通的, 这样的做法充分说明科学的理论是互相佐证的。并且给出两种直观解释。
一.用“均熵方程”导出温度梯度关系式
前人对准孤立体系的平衡态的描述强调指出,
在外场中, 即使体系内出现压强梯度、密度梯度,
也不应该存在温度梯度。
现在本文就依“均熵方程”式来讨论这个问题,
为了讨论的简便, 不妨暂以理想气体为例, 理想气体的比熵[1]也可表为
![]() (1)
(1)
(1) 式中, CP°(CP/m) 表示“等压比热”, CP为定压“摩尔热容”常数,R为气
体常数,m为理想气体摩尔质量, T为某点温度,P为该点压强。
将
![]()
![]() 代入(1) 式可得[2]
代入(1) 式可得[2]
![]() (2)
(2)
(2) 式中, γ为比热比, CV°(CV/m)
为“等容比热” 常数。
将(2) 式代入“均熵方程”整理得
![]() (3)
(3)
(3) 式中, ▽T为温度梯度, ▽P为压强梯度,(3)
式表明温度梯度与压强梯度相互依存。
由流体的静力平衡(匀强力场)
条件
▽P+ρg=0
(4)
对于无力场空间(g=0), 由(4)
式可知, ▽P=0, 再注意(3) 式可明白, 无力场空间中的准孤立体系的平衡态,
体系内必有▽T=0, 即为热平衡态(狭义平衡态)。
而在等势面上,虽然g≠0, ρ≠0,
但因等势面内的曲线总与场力线正交, 即有
![]() , 故有
, 故有
![]() , 则有
, 则有
![]() (5)
(5)
(5)式表明在等势面内任何方向压强梯度都为零。故在等势面上,
必有
![]() 即在等势面上的这个二维体系也无温度梯度,
即处于狭义平衡态。
即在等势面上的这个二维体系也无温度梯度,
即处于狭义平衡态。
在匀强力场作用下,
单元理想气体内的温度梯度表达式可由(3) 式结合(4) 式导得[3]
![]() (≠0)
(6)
(≠0)
(6)
在推导(6) 式中利用了关系式:ρV°=1,
PV°=RT/m, γ= CP° / CV°,CP°
- CV°
=R/m (6) 式就是其温度梯度表达式, 该式清楚地反映了在匀强力场中绝热平静的理想气体内存在着永恒的温度梯度(广义平衡态),负号表明其温度分布是依其参考高度递减的,
它所描述的这种温度梯度是由力场导致的(不需热源来维持),与热源无关,这里当然不存在传导热流,即无熵流伴随,
更无熵产生, 属定熵状态, 或曰不需付出耗散性代价。
另外,“均熵方程”可与“比势焓平衡方程”及“物态方程”联立成热力学方程组(类似于电磁学中的麦克斯韦方程组) :
▽s°=0(均熵方程)
(7)
▽H°+g=0(比势焓平衡方程)
(8)
F(T,P,ρ)=0(物态方程)
(9)
(7)
、(8) 、(9)三个独立的方程联立,
即可唯一地确定平衡态流体内的温度、密度、压强分布函数。有了,
也只有这样才算严格规范地解决了所谓流体系统终极态的性征,
否则,
一切凭经验或主观臆定的所谓平衡态原理均欠理论上的谨严性。
参考文献
[1]朗道·栗弗席兹(前苏联) 著
杨训恺等译 1964统计物理学(人民教育出版社)
90
(
Landau,L、D、and Lifshitz E、M、,Statistical Physics,Pergamon Press,1958,)
注释
[2] 理想气体比熵s°可表为
s°=CP°lnT-(R/m)lnP,
(10)
将γ=
CP° / CV°
, 及CP° - CV° =R/m代入(10)
式得
CP°lnT-(R/m)lnP=CP°lnT-(CP°-
CV°)lnP,
→(
CP° / CV°)lnT-[(CP° -CV°)/
CV°]lnP=γlnT-(γ-1)lnP,
故有
![]()
[3] 把①、ρV°=1, ②、PV°=RT/m, ③、γ= CP° / CV°, ④、CP° - CV° =R/m 代入下式
![]() (11)
(11)
①
式代入(11)
式得
![]()
②
式代入
![]()
③
式代入
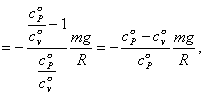
④式代入
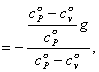
∴
![]()