宇宙整体时空结构与类星体红移的周期性分布
邓晓明
《潜科学》杂志 1993年 第1期
提要
本文进一步证明了类星体红移的周期性分布是宇内同一演化物质的不同年代像的反映;利用功率谱方法可以检测出样品中所有演化物质各自所表现的红移周期性的综合效果,但检测的结果与样品的选取直接有关,即并不是所有样品都能被检测出这种周期性成份。
关键词:宇宙模型、大尺度时空结构、红移、类星体
一、引言
围绕类星体红移周期性分布的论争可以一直追溯到发现大红移量类星体的60年代晚期,其焦点基本上是关于这种红移是否为宇宙论性的。Burbidge![]() 等人早在1967年就指出类星体的红移存在着某种周期性,随后Cowan
等人早在1967年就指出类星体的红移存在着某种周期性,随后Cowan![]() 、Lake和Roeder
、Lake和Roeder![]() 、Karlsson
、Karlsson![]() 、方励之、褚耀泉等
、方励之、褚耀泉等![]() 、Depaquit、Pecker和Vigier
、Depaquit、Pecker和Vigier![]() 、朱杏芬和褚耀泉
、朱杏芬和褚耀泉![]() 的研究结果都证实了红移确实存在着周期性分布的成份。对于这种在宇宙大尺度结构上表现的所谓“不均匀”性,有些作者把其归结为选择效应。其中最有代表性的文章是最近由D.Scott
的研究结果都证实了红移确实存在着周期性分布的成份。对于这种在宇宙大尺度结构上表现的所谓“不均匀”性,有些作者把其归结为选择效应。其中最有代表性的文章是最近由D.Scott![]() 发表的。
发表的。
本文证明所有类星体的红移都是宇宙的超球结构所决定的宇宙学红移![]() ,而类星体红移分布的周期性是与宇宙学原理相容的;类星体红移的周期性分布是各个宇内同一演化物质红移周期性分布的综合表现,是其在不同年代像的反映,是可以利用功率谱方法检测到的,但检测的结果与样品的选取直接有关。
,而类星体红移分布的周期性是与宇宙学原理相容的;类星体红移的周期性分布是各个宇内同一演化物质红移周期性分布的综合表现,是其在不同年代像的反映,是可以利用功率谱方法检测到的,但检测的结果与样品的选取直接有关。
二、功率谱方法与样品的选择
我们定义了宇内同一演化物质的概念![]() (以下简称演化物),并给出了描述其红移现象的红移公式或红移周期公式
(以下简称演化物),并给出了描述其红移现象的红移公式或红移周期公式![]() :
:
![]() (1)
(1)
![]() .
. ![]() ;
; ![]() (2)
(2)
这里![]() 为第
为第![]() 个演化物距我们最近像(第1个像)的红移值,
个演化物距我们最近像(第1个像)的红移值,![]() 为该演化物第
为该演化物第![]() 个像的红移值;
个像的红移值;![]() (
(![]() )为该演化物的初相角
)为该演化物的初相角![]() ,
,![]() 为红移周期参数
为红移周期参数![]() 。
。
由(1)式可见![]() 可以确定第
可以确定第![]() 个演化物相对地球的空间位置,由此我们定义其空间坐标为:
个演化物相对地球的空间位置,由此我们定义其空间坐标为:
![]() ,
,![]() .
(3)
.
(3)
根据宇的超球性质,由(3)式我们规定如果在任意两个观测方向上的两个演化物![]() 和
和![]() 的
的![]() 和
和![]() 相等(
相等(![]() ),则它们的空间坐标也相等(空间坐标
),则它们的空间坐标也相等(空间坐标![]() 在此可理解为相当于二维球面上的纬坐标,而观测者在该球面的极点上)。
在此可理解为相当于二维球面上的纬坐标,而观测者在该球面的极点上)。
变换(1)式得第![]() 个演化物的红移分布为:
个演化物的红移分布为:
![]() .
(4)
.
(4)
可以看出给定某一演化物的空间坐标![]() (
(![]() ),就可以由(4)式描述其红移序列
),就可以由(4)式描述其红移序列![]() .
.
下面我们将证明样品中所有演化物(类星体→星系)各自所表现的由(4)式所决定的红移分布的周期性可以通过统计方法检测出它们的综合效果。
功率谱方法最初由Yu和Peebles![]() 引入,被Lake和Roeder
引入,被Lake和Roeder![]() 第一次应用到红移分布问题上。目前该方法是检测类星体红移周期性成份的有效方法。对于变量
第一次应用到红移分布问题上。目前该方法是检测类星体红移周期性成份的有效方法。对于变量![]() 分布的功率谱定义为:
分布的功率谱定义为:
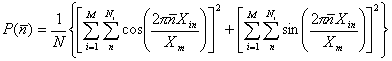 . (5)
. (5)
这里![]() 是类星体(也包含星系)样品总数,
是类星体(也包含星系)样品总数,![]() 为该组样品中的演化物数,
为该组样品中的演化物数,![]() 为第
为第![]() 个演化物被我们观测到的像数(注意:随机观测会出现某一演化物的像在
个演化物被我们观测到的像数(注意:随机观测会出现某一演化物的像在![]() 项上的破缺。例如我们只能观测到
项上的破缺。例如我们只能观测到![]() 和
和![]() ,而观测不到它的
,而观测不到它的![]() 、
、![]() 、
、![]() 、和
、和![]() 等,这符合我们观测的实际情况,因此
等,这符合我们观测的实际情况,因此![]() 一般为不连续的正整数),
一般为不连续的正整数),![]() 中的
中的![]() 是第
是第![]() 个演化物的第
个演化物的第![]() 个像的红移值,
个像的红移值,![]() 是波数,
是波数,![]() 是全部样品对应的
是全部样品对应的![]() 所占据的范围。由(1)式有:
所占据的范围。由(1)式有:
![]() .
(6)
.
(6)
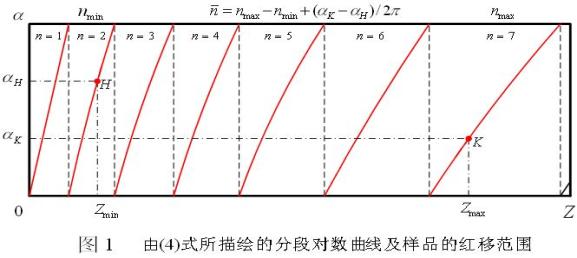
如果我们设所有样品(类星体或星系)的红移分布都由(4)式决定,则所有样品都会落在图1所示的分段自然对数曲线上。设H点和K点分别为一组样品中最小红移和最大红移样品,其他样品的红移都满足
![]() . 设与
. 设与![]() 所对应的周期数为
所对应的周期数为![]() ,其空间坐标为
,其空间坐标为 ![]() (
(![]() );与
);与![]() 所对应的周期数为
所对应的周期数为![]() ,其空间坐标为
,其空间坐标为![]() (
(![]() )。由(4)式得:
)。由(4)式得:
![]() ;
;![]() . (7)
. (7)
最后有:
![]() .
(8)
.
(8)
将(6)及(8)式代入(5)式得:
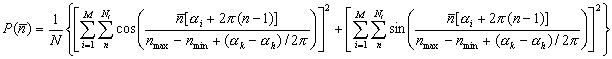 .
.
(9)
这里![]() 为任意正整数,若设
为任意正整数,若设
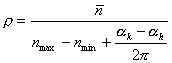 ,
(10)
,
(10)
则(9)式变为:
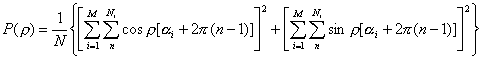 . (11)
. (11)
(10)式中的![]() 为非整周期数,且有
为非整周期数,且有![]() ,参看图1,可以证明功率谱中的波数应等于周期数
,参看图1,可以证明功率谱中的波数应等于周期数 ![]() ,即
,即 ![]() . 由(11)式可以证明当一组样品的
. 由(11)式可以证明当一组样品的 ![]() 足够大(一般应有
足够大(一般应有 ![]() )及其空间坐标
)及其空间坐标![]() 分布的非常集中时,功率谱将在
分布的非常集中时,功率谱将在![]() 处出现明显峰值,相应地(11)式变为:
处出现明显峰值,相应地(11)式变为:
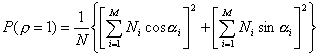 .
(12)
.
(12)
这时周期为:
![]() .
(13)
.
(13)
我们曾定义![]() 为单个演化物的红移周期参数
为单个演化物的红移周期参数![]() ,而(13)式中的
,而(13)式中的![]() 为样品中各演化物红移周期性分布统计的平均效果。可见,只要样品选择的适宜,其红移周期就接近于红移周期参数
为样品中各演化物红移周期性分布统计的平均效果。可见,只要样品选择的适宜,其红移周期就接近于红移周期参数![]() 。在此我们规定满足(12)式所需条件的样品为理想样品。
。在此我们规定满足(12)式所需条件的样品为理想样品。
一般情况下一组样品的![]() 分布具有一定的幅度,由(11)式可知功率谱不一定会刚好在
分布具有一定的幅度,由(11)式可知功率谱不一定会刚好在![]() 处,而是在某个
处,而是在某个![]() 处出现明显峰值。由(10)式得
处出现明显峰值。由(10)式得 ![]() ,如果把这时的周期记为
,如果把这时的周期记为![]() ,则有:
,则有:
![]() .
(14)
.
(14)
由此可见周期![]() 与红移周期参数
与红移周期参数![]() 有个偏差。参看图1,我们可以计算
有个偏差。参看图1,我们可以计算![]() 的可能取值范围。
的可能取值范围。
![]()
![]() ,则
,则 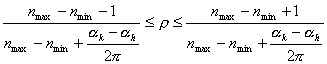 ,
,
又 ![]() ,
,![]()
![]() . (15)
. (15)
由(15)式可以看出![]() 越大,
越大,![]() 的取值范围越临近于1。另外,由(14)式还可以得到
的取值范围越临近于1。另外,由(14)式还可以得到![]() 的取值范围,而且可以看出
的取值范围,而且可以看出![]() 越大,
越大,![]() 越临近于
越临近于![]() 。如果设红移周期参数
。如果设红移周期参数![]() ,我们可以得到表1的计算结果。
,我们可以得到表1的计算结果。
表1 ![]() 及
及![]() 的取值范围(设
的取值范围(设![]() )
)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
若考虑到大部分具有红移周期性分布成份样品的功率谱都在大于或等于5的某个波数上取得明显峰值,我们取![]() ,这时由表1可知
,这时由表1可知![]() 的范围是:
的范围是:
![]() .
.
对于一组随机分布的变量,如果我们计算![]() 的
的![]() 组值(见(9)式),
组值(见(9)式),![]() ,则其中有任何一个值大于
,则其中有任何一个值大于![]() 的几率为:
的几率为:![]() 。对于
。对于![]() ,周期性分布的统计置信度为:
,周期性分布的统计置信度为:![]() . 虽然目前对
. 虽然目前对![]() 的取值尚有争议
的取值尚有争议![]() ,但我们可以看出对于一组给定样品,
,但我们可以看出对于一组给定样品,![]() 值越大,其置信度越高。
值越大,其置信度越高。
而由(11)式可以看出![]() 值的大小取决于
值的大小取决于![]() 的分布状态。
的分布状态。![]() 分布的越集中,
分布的越集中,![]() 值越大,相应地,该组样品红移周期性分布的统计置信度也越高。
值越大,相应地,该组样品红移周期性分布的统计置信度也越高。
综上所述,在假定所有样品的红移分布都由(4)式所决定的情况下,我们知道样品的优劣取决于其内各演化物空间坐标![]() 的分布状态,及其红移的范围(
的分布状态,及其红移的范围(![]() ,
,![]() )或(
)或(![]() )。
)。![]() 分布的越集中,
分布的越集中,![]() 越大,周期
越大,周期![]() 越接近于红移周期参数
越接近于红移周期参数![]() .对于理想样品有
.对于理想样品有![]() .相反,若
.相反,若![]() 在区间[
在区间[![]() ]分布的较均匀,功率谱的均值及方差将等于1.
]分布的较均匀,功率谱的均值及方差将等于1.
三、典型样品的分析
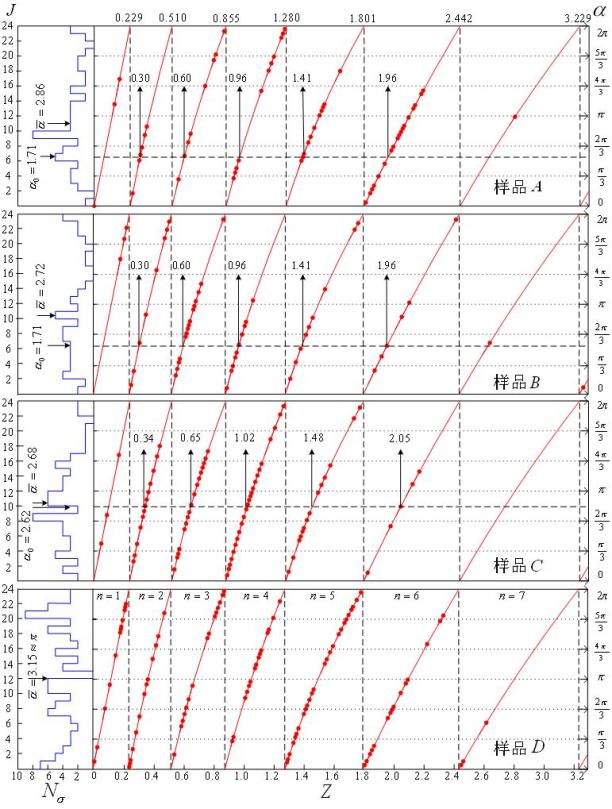
鉴于大部分具有红移周期性成份样品中的分析结果都呈现 ![]() ,在此不妨把其接受为红移周期参数的真值。下面我们将对5个典型样品进行分析。样品A为Multiple QSOs
,在此不妨把其接受为红移周期参数的真值。下面我们将对5个典型样品进行分析。样品A为Multiple QSOs![]() ;样品B为 Oh Radio QSR’s
;样品B为 Oh Radio QSR’s![]() ;样品C为 12h Radio QSR’s
;样品C为 12h Radio QSR’s![]() ,样品D为 Extragalactic emission-line objects
,样品D为 Extragalactic emission-line objects ![]() ;样品E为 LBQS
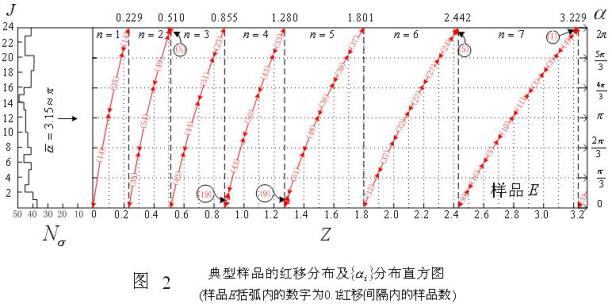
;样品E为 LBQS![]() 。图2中的右图为由(4)式所决定的各组样品的红移分布;左图为各个演化物空间坐标
。图2中的右图为由(4)式所决定的各组样品的红移分布;左图为各个演化物空间坐标![]() 在区间[
在区间[![]() ]的分布直方图,其
]的分布直方图,其![]() 的间隔为
的间隔为 ![]() ,则在区间[
,则在区间[![]() ]内共有24个间隔。
]内共有24个间隔。![]() 是演化物数,
是演化物数,![]() 是
是![]() 的均值,即
的均值,即 ![]() ,
,![]() 是样品原来红移峰值所对应的空间坐标,在此我们称其为样品的相。由前节的讨论我们知道
是样品原来红移峰值所对应的空间坐标,在此我们称其为样品的相。由前节的讨论我们知道![]() 围绕其均值
围绕其均值![]() 的集中程度可以衡量某组样品的质量。在此我们定义:
的集中程度可以衡量某组样品的质量。在此我们定义:
![]() ,
, ![]() (16)
(16)
这里![]() 是
是![]() 所对应的间隔数,
所对应的间隔数,![]() 是以
是以![]() 点为对称的
点为对称的![]() 点两边的间隔数(区间长度),
点两边的间隔数(区间长度),![]() 是间隔数,
是间隔数,![]() 是第
是第![]() 个间隔内的演化物数,
个间隔内的演化物数,![]() 是在区间
是在区间![]() 内演化物数占样品中总演化物数的百分比。很明显通过计算各组样品的
内演化物数占样品中总演化物数的百分比。很明显通过计算各组样品的![]() 值,我们可以把握
值,我们可以把握![]() 围绕
围绕![]() 的集中程度。
的集中程度。
图3给出了各组样品的![]() 分布,从中可以看出样品A、B和C较样品D和E的
分布,从中可以看出样品A、B和C较样品D和E的![]() 分布的集中,由图中各组样品的
分布的集中,由图中各组样品的![]() 曲线凸的程度我们可以评价在检测红移分布的周期性时,样品A、B和C是较好的,而样品D和E的
曲线凸的程度我们可以评价在检测红移分布的周期性时,样品A、B和C是较好的,而样品D和E的![]() 在区间[
在区间[![]() ]接近均匀分布,因此没有明显的周期性。这也和我们通过功率谱方法所得到的结果相一致。
]接近均匀分布,因此没有明显的周期性。这也和我们通过功率谱方法所得到的结果相一致。
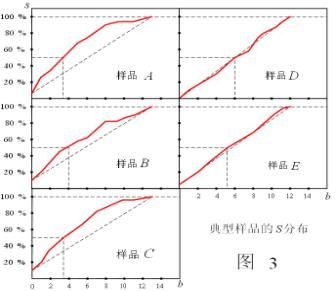
样品A、B和C的![]() 在区间[
在区间[![]() ]分布的非均匀性暴露了其内各演化物所表现的红移周期性的综合效果。而样品D和E则相反,特别象样品E这样大的样品数(由1026个样品组成),会淹没各演化物所表现的红移周期性质。由图2,我们可以看出样品C相对样品A和B的相移是由其
]分布的非均匀性暴露了其内各演化物所表现的红移周期性的综合效果。而样品D和E则相反,特别象样品E这样大的样品数(由1026个样品组成),会淹没各演化物所表现的红移周期性质。由图2,我们可以看出样品C相对样品A和B的相移是由其![]() 的分布状态所决定的,因此说随各组样品的
的分布状态所决定的,因此说随各组样品的![]() 的分布状态的不同其相
的分布状态的不同其相![]() 也不同,由计算得样品A和B的相
也不同,由计算得样品A和B的相 ![]() (孤度),样品C的相
(孤度),样品C的相 ![]() (孤度)。
(孤度)。
四、综述及结论
通过以上讨论,特别是对典型样品的分析,我们清楚地知道不可能通过在地球上的观测得到某一演化物的完整周期像,而只能把各个演化物所表现的红移周期性质综合起来通过统计的方法检测到。
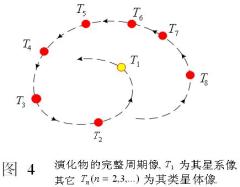
虽然宇宙物质在宇内整体上呈现动力学意义上的静态,但在局部空间内确充满着运动,事实上正是由于各星系的本动才使我们能有机会看到它们的过去。对此我们可以这样描述;参看图4,设我们地球(观测者)的位置垂直于图面以上,虚线所描述的轨迹是被观测到的某一演化物在垂直于我们视线平面上的本动轨迹。设宙![]() 时的像为该演化物距我们最近的像(星系像),相应地宙
时的像为该演化物距我们最近的像(星系像),相应地宙![]() 、
、![]() 、
、![]() 、
、![]() …时的各重像(类星体)也在图中给出。当然该演化物在任意宙
…时的各重像(类星体)也在图中给出。当然该演化物在任意宙![]() 时所发射的电磁波在绕超球面上的大园运动时,有的像会被别的演化物掩掉,或被其本身掩掉。这样我们就会失去它的完整周期像。当然也可能在这一视线方向上存在两个或若干个演化物,使得它们的各重像相互混杂,这也为我们观测到(或判断出)某一演化物的完整周期像增加了困难。然而,这种描述的结果会使我们得到在亮星系周围会有更多的类星体的结论。这也为观测所支持
时所发射的电磁波在绕超球面上的大园运动时,有的像会被别的演化物掩掉,或被其本身掩掉。这样我们就会失去它的完整周期像。当然也可能在这一视线方向上存在两个或若干个演化物,使得它们的各重像相互混杂,这也为我们观测到(或判断出)某一演化物的完整周期像增加了困难。然而,这种描述的结果会使我们得到在亮星系周围会有更多的类星体的结论。这也为观测所支持![]() 。
。
基于以上的讨论,我们知道各演化物所表现的红移周期性质是可以通过一定数量的样品,由统计的方法检测出它们的综合效果,但样品的选择至关重要。Arp等人多年来一直从事在亮星系周围寻找类星体的工作,至今已经积累了许多例子。这是因为在亮星系附近的类星体是其早期重像(参看图4)的可能性最大,由此所得到的样品(如样品A)应该具有更明显的红移周期性。可以说全天区的随机观测或将各子样品随机组合得到的大样品(如样品E)将减弱或淹没红移的周期性质。
对于红移样品的特性,有如下结论:
(1)样品内演化物空间坐标![]() 绕其均值
绕其均值![]() 分布的越集中,其功率谱的峰值越明显,相应地置信度也越高。样品的红移范围(
分布的越集中,其功率谱的峰值越明显,相应地置信度也越高。样品的红移范围(![]() ,
,![]() )或(
)或(![]() )越大,
)越大,![]() 值越临近于1(非整周期数
值越临近于1(非整周期数![]() 的影响越小),相应地红移周期
的影响越小),相应地红移周期![]() 越接近于红移周期参数
越接近于红移周期参数![]() 。若设
。若设![]() 的集中程度不变,则
的集中程度不变,则![]() 越大,
越大,![]() 的分布相对地变窄。
的分布相对地变窄。
(2)样品的相![]() 是由其
是由其![]() 的分布状态所决定的,即随各样品的
的分布状态所决定的,即随各样品的![]() 分布的不同会有相移。
分布的不同会有相移。
[致谢]:本文以通信的方式在与瑞典天体物理学家K.G.Karlsson博士的讨论中形成的,在此向他表示衷心的感谢;同时对远在德国的毕红光博士和H.Arp博士的来信及他们在信中对这项工作所表示的极大兴趣和提出的良好建议致以衷心的感谢。
参考文献
[1]Burbidge,G.R.,Burbidge,E.M.:1967,Ap.J.Lett.,148,L107
[2]Cowan,C.L.:1969,Nature 224,665
[3]Lack,R.G.,Roeder,R.C.:1972,J.R.Astron.Soc.Canda 66,111
[4]Karlsson,K.G.:1977,Astron.Astrophys.58,237
[5]方励之,褚耀泉等:1982,A.Ap.106,287
[6]Depaquit,S.,Pecker,J.C.,Vigier,J.P.:1981,Astron.Nach.306,31
[7]朱杏芬,褚耀泉:1990,天文学报31,132
[8]Scott,D.:1991,Astron. Astrophys.242,1
[9]邓晓明:1992,潜科学杂志1,35
[10]邓晓明:1992,潜科学杂志5,24
[11]Yu,J.T.,Peebles,P.J.E.:1969,ApJ158,103
[12]Arp,H.,Bi,H.G.,Chu,Y.,Zhu,X.:1990,Astron.Astrophys.239,33
[13]Cristiani,S.,Barbieri,C.,lovino,A.,La Franca,F.,Nota,A.:1989,Astron.Astrophys.
Suppl.
[14]褚耀泉,朱杏芬,Burbidge,G.,Hewitt,A.:1984,A.Ap130,408