论宇宙的几何及物理特征

论宇宙的几何及物理特征

邓晓明

《潜科学》杂志 1992年第5期

提要

本文通过类星体红移周期性分布的观测统计结果证明宇宙时空在整体上呈超球结构，从而排除了Friedmann模型另外两种空间形式存在的可能性；引入了和哈勃常数具有同等近似程度的重要观测参量,并由此得到所有宇宙几何参量的数值解。

关键词：宇宙模型、大尺度时空结构、红移、类星体

一、引言

根据宇宙学原理，我们可以构造3种可能的空间度规形式。到底哪一种与我们宇宙的实际空间结构性质相符合？对此本应借助宇宙动力学通过天文观测来确定。然而目前减速因子和宇宙物质平均密度之间的观测矛盾致使Friedmann模型也在宇宙的“闭”与“开”问题上陷入了困境。

类星体红移周期性分布的观测统计结果暴露了宇宙整体时空结构的重要信息并由此证实Friedmann宇宙中的超球解是唯一符合宇宙实际空间性质的。

对于宇宙整体时空性质，我们在此没有必要拘泥于牛顿时空和爱因斯坦时空的哲学讨论，因为利用牛顿理论也可得到同样的宇宙动力学演化方程。为了理论上的需要，如果我们把宇宙整体时空结构看作为4维欧氐空间中的超球，其鲜明的物理意义为：3维超球面是宇宙整体空间；其半径是宇宙尺度因子，这里矢量与时间矢同向且处处正交于空间。

二、相关公式的推导

1、红移公式：

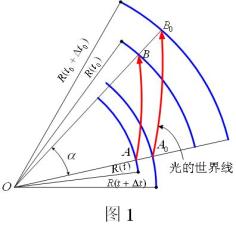
参阅图1，设处光源于时刻（点）发出一波前，光传播到的时刻为：（点），由，得：

，（1）

一周期后，另一波前从时刻（点）传播到的时刻为：（点），则有：

，（2）

由于（1）和（2）式积分项中的相位角不变，则：，由于，所以：

，（3）

2、哈勃常数：

对于附近星系发出的光，其传播距离为（从点到点）：

，（4）

由图1的几何关系可知：

，（5）

将（3）式代入（5）式得：

，（6）

定义哈勃常数为：

或，（7）

并将（4）式代入（6）式得哈勃定律：

. （8）

3、红移周期公式

如果我们考虑这样一个历史时期，宇宙半径的增长速度缓变，即（是常数），则有：

，. （9）

由（1）式得：

，（10）

积分得：

，（11）

由（3）式得：

，（12）

由于光子在膨胀的超球面上不断绕行，令及，最终我们可由（12）式得到红移周期公式（具体推导过程请看邓晓明，1992年文章[1]）：

，（13）

其中.

三、，Friedmann超球模型与的内在联系

无压（）宇宙演化方程可写为：

，（14）

或，（15）

这里是宇宙物质总量且为常数；是宇宙空间体积。

解（14）和（15）式并引入一个展开角得：

，（16）

，（17）

. （18）

这里是宇宙半径（尺度因子）的增长速度，其中 .令、、0，1，2，… . 由此可知是一个周期函数。由（16）及（17）式可知，宇宙半径的最大值：

（）. （19）

宇宙寿命期（周期）：

. (20)

如果我们把做为一个观测参量，则由(7)式得：

，（21）

由于距现在较近的一定历史时期内，[，]，可看作为一个缓变函数（后面的分析将证明这种处理是合理的），因此有：

，处（22）

这里是时空当量为一常数，其值为：

，（23）

其中是红移周期参数，是光速。将（23）式代入（22）式得：

，（24）

由（21）式可知：

，（25）

若取宇宙减速因子的测量值；哈勃常数；，则解（16）、（17）、（18）、（24）及（25）式得：

宇宙现在的半径：光年；

宇宙年龄：秒年；

宇宙半径现在的增长速度：.

由（19）和（20）式得：

宇宙最大半径：光年；

宇宙的寿命周期：秒年.

至此似乎我们已经得到了所有宇宙几何参量的数值解。由宇宙整体时空拓扑，我们把Friedmann模型限定在超球解，而类星体红移周期性分布的观测结果则是对这一假设的直接验证。由此我们可以得出宇宙物质现在的平均密度一定大于临界密度的结论，即. 由于的测量值比其它参量的不确定程度大，因此我们不妨用对其进行计算。如果我们相信，则有：

或 . （26）

如果我们有兴趣，由（15）式可求出宇宙物质总量：

(26)式中的计算结果与其实测值的差值为宇宙论明确了寻找失踪质量的任务。

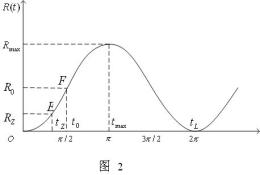
由方程(16)和(17)所描述的参数曲线参看图2. 其中点为宇宙年龄和宇宙半径的坐标点。由于类星体的红移样品绝大多数都落在红移范围之内，因此对这段历史时期进行考查是十分有意义的。由红移公式(3)可知：

光年。相应地，当时的时刻年。该坐标点用来表示。

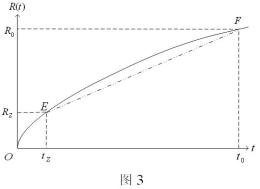
为了进一步考查曲线，明确与之间的关系，我们把其从图2中摘出，并用坐标描述。图3中的曲线给出了从宇宙创生后的17亿年到现在（114亿年）这段历史时期内（也可称其为类星体到星系的演化时期）随增长的变化情况。

表1

（亿光年）	（亿年）
6.56	114	0	0	0.0328C	1
6.06	99	0.082	0.6%	0.0354C	1.079
5.56	86	0.180	2.2%	0.0382C	1.165
5.06	73	0.296	7.2%	0.0414C	1.262
4.56	62	0.438	16.7%	0.0449C	1.369
4.06	51	0.616	24.4%	0.0490C	1.494
3.56	41	0.843	36.1%	0.0537C	1.637
3.06	32	1.144	58.9%	0.0595C	1.814
2.56	25	1.562	78.3%	0.0666C	2.030
2.05	17	2.200	98.3%	0.0762C	2.323

表1给出了随时间或红移变化的计算结果。其中是所选择的3个典型类星体红移样品（低红移星系周围多重类星体和）的样品总数，是该样品在红移以内的样品数，则是在红移范围以内的样品数占样品总数的百分比。该表的计算结果表明从17亿年到114亿年这段宇宙历史时期内确为一个缓变函数（由于是红移周期的统计平均值，而我们令，所以这是个保守的估计）。与的偏离程度由来描述。因此在这一历史时期内（22）式是近似成立的。事实上与的偏离程度也正是哈勃常数在这一历史时期内的偏离程度。因为由哈勃常数的定义式（7）可知：

或 .

也就是说宇宙论中用所计算的结果与用或所计算的结果其近似程度是一样的。

总之，在17亿年到114亿年这一历史时期内设或的意义不但在于简化了数学处理上的困难，更重要的是这种处理手段可直接从理论上推导出Karlsson在1971年及后来通过观测资料的统计分析所得到的经验公式[参看(13)式]，并且为宇宙论提出了另一个和哈勃常数具有同等近似程度的观测参量，从而确定了宇宙在这一时期内的Friedmann超球演化模型。

四、综述与结论

我们知道宇宙早期的能量供献以辐射为主()。这一时期的行为也应该为Friedmann超球模型所描述。在光子与物质退耦后，宇宙能量供献开始变为以物质为主。在此以后，从17亿年（当然可能再早些，因为已发现了许多的类星体）到114亿年的这段时间可以认为是类星体到星系的演化时期。通过前面的讨论，我们知道这一时期的行为由的Friedmann超球模型所描述。如果说宇宙早期所遗留下来的氦丰度和微波背景辐射是Friedmann超球模型的观测证据，那么类星体红移周期性分布的观测统计结果则是对其的又一验证。