说明：下面的文章（上、中、下）发表在《物理与工程》杂志2002年12卷4、5、6期上

作者简介：张学文1935年生于天津，1957年从北京大学毕业后即到新疆气象局从事科技工作到1998年退休.研究员，原新疆气象研究所所长.曾热心于把分布函数概念和熵原理应用于物理学以外的气象等领域，写过一些论著，组织过“全国熵与交叉科学研讨会”，编辑过文集，提出过熵就是客观事物的复杂程度，熵原理就是复杂程度自动地最大化等论点.退休后创办“熵、信息、复杂性”（ http://entropy.com.cn ）等网站，以讲座形式介绍有关认识.2001年把讲座改称为“组成论”.《组成论》全书22章（将要在2003年7月由新疆教育出版社出版）--2002.11

组成论介绍（上）：广义集合和分布函数(a)

张学文

zhangxw@mail.xj.cninfo.net

（新疆气象科学研究所，830002）

  2002年11月公布于潜科学网站

摘  要 从天体到原子都存在内部组成问题.组成论为研究各种组成问题提供一般模型、概念、方法和规律.组成论把“分子由原子组成”的认识泛化为更一般的模型，并且称它为广义集合.每个广义集合都伴有一个分布函数.用分布函数可计算出度量系统状态丰富程度的一个物理量--复杂程度.具有随机性的事物的复杂程度会自动的最大化（熵原理）.利用这种最大化可以反求很多公式.组成论是从新视角分析事物的知识框架.

关键词 组成 熵 信息 复杂性

1. 组成问题

近代自然科学分为天文、地理、物理、化学、生物等学科，而这种分科竟有上千种.当今“分科日细”的趋势固然要继续下去，但“只见树木不见森林”的倾向也妨碍了对客观事物的共同规律的探求.

难道放弃上述科学分科，横向地观察客观事物，就不存在普遍性的概念和规律吗？笔者提出的组成论试图说明一般的客观事物也有其通用的模型、概念和规律.

天文学分析天体的组成、地质学分析地壳的组成、化学家分析分子的组成、物理学分析原子的组成、生物学分析生物物种的组成.再者，中国由那些省区组成、社会由那些阶级组成、一付中药由那些药材组成、一本书由那些章组成、一个演出由那些节目组成、一个体操由那些动作组成等等也都是组成问题的特例.看来，一切领域都存在组成问题.

过去各个学科仅研究本领域所特有的组成问题，不同学科研究组成问题的观点、概念、方法、技术方面是否存在共同规律的问题没有多关注.组成论把各个领域的组成问题一般化，寻找其一般模型和共同规律.

10年前笔者曾提出“统计物理中的深刻思想不应当仅供物理学家独享，它实际上也是众多学科共享的理论武器.它会帮助众多学科向理论阵地迈进一大步”^[1]的看法.组成论是这种认识的深化.组成论目前主要涉及“广义集合”、“分布函数”和“复杂程度”这三个概念和最复杂原理（对熵原理的准确又通俗的称谓）.

2. 客观事物的广义集合模型

组成论为认识客观事物提供一个非常简单的数学模型--广义集合.如果某事物符合这个模型就归入研究范围，否则暂不过问.广义集合既度量物质的数量也区分性质的差别，它是哲学上的客观事物的具体化和自然（社会）科学研究对象的抽象化.

2.1概念的引入

数学领域的集合论也研究组成问题，它根据一个总体内的某种性质的差别把总体分成了两两彼此不同的若干个个体（称为元素）.它的一个弱点是不便描述相同元素的数量的差别.如框图中有两个a和4个b .集合论仅说它有两种不同的元素（a，b）不过问每种元素各有多少.

图1. 广义集合和集合都描述集体，但是前者更精确些  

   集合语言指明水由氢和氧两种元素组成，不回答水分子由几个氢原子几个氧原子组成.广义集合不仅要明确一个集合内的两两相异的元素（改称为标志）有那些，还要明确每种元素有多少个（引入个体的概念）.广义集合把集合论中的元素概念分裂为个体概念和标志（值）概念.

2.2“个体”概念----强调彼此地位相同

一副麻将牌是一个总体（群体），尽管每张麻将牌的正面可能不同，但是它们的被面却完全相同.如果仅从被面看这个总体（群体），它里面就包括着很多完全相同的个体.“个体”二字强调各个个体的全同性.在物理学和化学中我们经常把各个电子（质子）都看作是完全相同的，它都是“个体”的例子.

表1.一些总体内的个体

在总体内的个体有时具有相对的不可再分性.在一些场合再细分就危及了这种个体的存在.例如有时一个人就是一个个体，把人再分，就失去人的含义了；把一张人民币看作是一个个体，再切分它就成了废纸.

“个体”概念强调同一总体（群体）内各个单元的“全同性”、“不可分辩性”.

2.3标志概念—描述差别

       个体概念强调了各个个体全同性这个侧面，但各个具体的个体在其他的侧面的特征可能相同也可能不同.从被面看，每张麻将牌都相同.但正面有“条”、“万”等等有不同的面孔.参加考试的每个考生的地位是相等的，但考分并不一定相等.为了描述一个总体内各个个体的某个属性的差别（不相同的侧面），还要引入标志概念（含义与集合中的元素概念基本相同）.

       标志是对总体内的每个个体都具有的某个属性、侧面、特征、指标（如身高）的描述.500万学生参加高考，语文成绩就是一种“标志”（描述了考生的一个侧面）.而每个个体（考生）就某某标志的具体取值（如语文成绩为85分）称为标志值.每个考生的成绩可能不相等，这说明标志值有能力描述各个个体之间在属性、形态、性质方面的差异性.

  表2.个体、标志和标志值举例

  表中的“体重、温度、价格”等等通称为标志、标志变量，而具体的体重37公斤、温度23度、价格15元、 “赞成票”、“三万”、“七饼”称为标志值.标志是对一种特征的通称，而标志值是对标志的取值的特称.

       标志概念强调每个个体要有确定值，（不能没有确定值，也不能有多个值）“标志”描述总体内部各个个体在形态、属性方面的差异性.

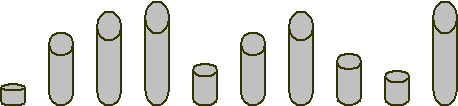
       有10个圆柱体，它们的横截面的直径都相同，但是高度却各不相同（不尽相同）.从“横截面的直径都相同”的角度看，每个个体是全同的.而每个圆柱体的高度不尽相同，体现了各个个体的差别性.高度是这个个体都具有的一种标志，其每个个体的标志值可能不同.

图2. 由10个圆柱体组成的一个广义集合

（横截面的直径都相同，体现了个体的全同性；  
圆柱体可能有不同的高度，体现了标志值的差异性）

§2.4广义集合

一个总体（系统、体系、群体、集体）如果可以区分成多个（≥0）地位相同的个体；就某个（可能多个）标志（属性）而言，每个个体都有确定的标志值，这个总体就是一个广义集合.

一个水分子由两个氢H原子和一个氧O原子（个体）组成，把每个原子看作是个体，把每个原子的原子量（氢原子是1，氧是16）看作是标志值，水分子就是一个广义集合.化学里有上百万种分子，它们都是广义集合的个例.一副麻将也是一个确定的广义集合，它由136张背面完全相同的个体（牌）组成，牌的正面上的“条、饼、万和风…”通称为标志，每张牌上的三万、五条等等都是具体的标志值.

电视屏幕的画面是由很多小点（象素）组成的.每个象素面积相同，可以视为一个个体.由于每个象素的颜色不尽相同，可以把“颜色”看作是标志，每个象素的具体颜色（红、黄…）就是标志值.所以每个屏幕画面都是一个广义集合.广义集合是描述总体（客观事物）内部某个标志（属性）的差异性和对应的数量多少的统一、简练、定量的模型.

描述广义集合的最基本（笨）的方法是给每个个体一个不重复的编号号码，再列出它的标志值.它就是一个仅有两列（或者行）的表.一列（行）是编号，另一列（行）是标志值.我们把它称为广义集合的原始列表.原始列表是广义集合的基础资料，也是对广义集合的完备描述（更丰富的关系广义集合无力描述）.

表3.一个班9名学生的成绩就是广义集合的原始列表

天文地理物理化学等学科在不同的层次上研究客观事物，广义集合和个体概念可以用在不同的层次上.一个恒星、一个电子可以是不同的广义集合中的个体.有的广义集合的标志值是数量，例如学生身高，有的广义集合的标志值不是数量，例如颜色、人的血型等.电脑语言中有字符串变量概念，一切标志值都可以用字符串变量表示.

广义集合概括客观事物的一种模型，符合这个模型的客观事物很多.但这也可能排斥了某些客观事物.分析客观事物是否符合这个模型固然是一种限制，但是看到每个广义集合都伴有一个“分布函数”（客观规律），我们又获得了回报.

分子由原子组成的学说（原子论）是现代科学的伟大成绩.组成论中的广义集合概念就是原子论学说的泛化.广义集合把分子由原子组成的层次关系推广到另外的场合中.

3. 送来的规律---分布函数

寻找规律是科学活动的内容.什么是规律？找出了变量之间的函数关系就得到了规律.测量了全校306个学生的体重，得到306个数据.这些数据不能说是规律.如果利用这些数据找出体重与年龄的某种函数关系，就认为得到了客观规律.确实，寻找函数关系（公式）经常是寻找规律的代名词. 现在要指出，每个确定的广义集合必然伴随着一个确定的“分布函数”，由于函数就是客观规律，每确定了一个广义集合也就送来了一个客观规律.

3.1分布函数

广义集合的定义本身埋伏了一个问题：一个广义集合内不同标志值的个体各有多少？分布函数就是对这个问题的答案的统称.

全校的学生是一个广义集合，每个学生是个体，把学生体重作为标志，可以得到表4.

表.4.不同标志值占有的个体的数量的例子

        表中的x 表示学生体重，n  表示在该档次中的学生人数.它回答了不同标志值的个体各有多少的问题.由于每个x 值（学生体重）都有唯一的n 值（学生数量）与它对应，说明它符合函数概念.这个函数体现了不同体重的学生如何分布在学生中，或者不同数量的学生是如何分布在不同的体重中的，所以称为分布函数.

分布函数是函数关系的一种，它揭示了广义集合（总体、系统、体系）内不同的标志值（x ）与其占有的个体的个数（n）的函数关系.

一个确定的广义集合就必然确定了不同的标志值的个体的数量是多少，即每个确定的广义集合必然伴随一个确定的分布函数.这是广义集合定义的自然推论.

3.2分布函数的例子