Long-term Memory in Climate Change in the East-Asian Monsoon

东亚季风气候变化的长期记忆性

Hong-xing Cao*¹   Richard Blender²   Hui-zhong He¹   Xiu-hua Cai¹

1Chinese Academy of Meteorological Sciences, 46 Zhongguancun Nandajie, 100081, Beijing, China

2 Meteorologisches Institut, Universitaet Hamburg, Bundesstrasse 55, D-20146 Hamburg, Germany

* E-mail: caohx@cams.cma.gov.cn

2004，04公布于潜科学网站

Abstract

The East-Asian monsoon is of slowly varying trend according to analyzing the observed time series of the monsoon index for 1873—2000. The detrended fluctuation analysis (DFA)is applied to the East-Asian monsoon, and its long-term memory is detected. In particular, the scaling exponent of the summer monsoon isα=0.73,which is much higher that of white noise(α=0.50); it implies there is a potential to advance the prediction skill of weather and climate over the monsoon region.

1 Introduction

As the weather and the climate in China and East-Asian, in particularly, in summer, such as Meiyu weather over Yangtze River in June, July, are strongly influenced by the East-Asian monsoon,. So predicting the intensity and duration of the summer East-Asian monsoon is important task for Chinese meteorologist. There have been a number of studies on the East-Asian monsoon and its prediction (Chen at al, 1991).The long-term memory of the monsoon hints better predictability of climate change, so the long-term memory provides a theoretical basis for its prediction.

An autocorrelation function C(s) of time series is regarded as an indication of its memory. Therefore, the analysis of correlations and its realistic physical modeling are fundamental in monsoon research. Recently, quantitative studies of the memory in atmospheric surface temperatures revealed that atmospheric surface temperature fluctuations exhibit long-term power law correlations C(s) ～ s^-γ with γ≈ 0.70 (Koscielny-Bunde et al., 1996; Koscielny-Bunde et al., 1998; Pelletier, 1997). The long-term persistence of the sea surface temperature (SST) is characterized by a correlation exponent γ= 0.4 for the Atlantic and the Pacific oceans, it is found that for all time scales the SST fluctuations exhibit stronger correlations than atmospheric surface temperature fluctuations (Monetti et al. 2002).  It is a vital conclusion that the global climate model are not able reproduce the observed long-term memory in global warming simulations, and thus raised concern about the relevance of the anthropogenic impact (Govindan et al. 2002).The spectral behavior of global surface temperature fields of 100-yr observations and a 1000-yr simulation of present-day climate with a complex atmosphere-ocean model using DFA has been analyzed, the power law scaling of near surface temperature fluctuations and its geographical distribution is determined (Fraedrich and Blender, 2003). The evidence of long-term memory in the NCEP (National Center for Environmental Prediction) observations and simulations using coupled atmosphere-ocean models with greenhouse gas increase according to the IPCC (Inter-governmental Panel of Climate Change) scenario in 1860-2099 has been found. In present context, we use the detrended fluctuation analysis (DFA) method (Peng et al., 1994; Kantelhardt et al., 2001) to study the long-term memory of the East-Asian monsoon, in order to understand the predictability of the monsoon climate.

2 Method

Observed time series are often highly nonstationary. A bounded time series can be mapped to a self-similar process by integration; for example, a sequence of coin flips can be mapped in this way to a one-dimensional random walk, a stationary integrated time series. The integration procedure will make the nonstationarity of the original data even more apparent. To overcome this complication, we have introduced a modified root mean square analysis of a random walk, termed detrended fluctuation analysis (DFA), which has been successfully applied to a wide range of a time series in recent years. Among the advantages of DFA over conventional methods (e.g., spectral analysis and Hurst analysis) are that it permits the detection of intrinsic self-similarity embedded in a seemingly no stationary time series, and also avoids the spurious detection of apparent self-similarity, which may be an artifact of extrinsic trends. Therefore the DFA is much useful for climatological analysis, as the DFA algorithm works well for certain types of nonstationary time series (especially slowly varying trends), such as some observed or a simulated climate series.

We calculate the departure seriesΔx(i) of the time series x(i),i=1,2,……N

Δx(i)= x(i)―<x>

where <x>is the average value of the series x(i) with the sample size N, and theΔx(i) with increasing i are integrated and denoted as y(k). i. e.

Then y(k) is divided into segments of equal length s and the least-square line fitting the data in each segment, y_s(k), is calculated. The series y(k) is detrended by subtracting the local trend y_s(k), and the root-mean square fluctuation F(s) of the detrended series is computed:

F(s) is computed for all “segment-size” s. If log F(s) increases linearly with log s, then the slope of the line relating F(s) and s in a log-log scale gives the scaling exponent α, a self-similarity parameter. This computation is repeated over all time scales (segment-sizes) to provide a relationship between F(s) and the segment-size s. Typically F(s) will increase with segment-size s. A linear relationship on a double log graph indicates the presence of scaling (self-similarity)—the fluctuations in small segments are related to the fluctuations in larger segments in a power-law fashion.

According to the random walk theory, the fluctuations function F(s) in a given time segment of length s are related to the autocorrelation function C(s) of time series. For the long-range power law correlation show a power spectrum:

C(s)~s^-γ, 0＜γ＜1

The fluctuations function F(s) increase as a power law:

F(s) ~ s^α, α=1－γ/2.

Forα=0.5, γ=1, the spectrum of the time series is white and forα=1, γ=0, the spectrum is 1/f(flicker )noise; between them the time series is nonstationary with long-term memory. Forα=1.5, γ= －1, it is Brownian noise, a pure random walk.

The DFA computations were made for the East-Asian monsoon and relevant analysis was carried out. In order to compare, the computations were also conducted using the derivative wavelet method (WL, Kovacevic, 1995) and the standard fluctuation analysis (FA, Monin and Yaglom, 1975).

3 Result

To view the climate change trend of the East-Asian monsoon, the least square line fittings for the East-Asian monsoon intensity index with sample size N, which was defined and calculated by Shi and Zhu (2000), were conducted. The trend of the winter monsoon is almost unchangeable for the sample from 1873 to 2000, i.e. the decrease of the winter monsoon is quite weak, its linear regressive coefficient is a = -0.00174. The decrease trend of summer monsoon is less weak, a = -0.0107 (Fig.1).So it is concluded that the East-Asian monsoon is of a slowly varying trend. Therefore, as mentioned above, the DFA algorithm works well for the East-Asian monsoon index time series. Thus the DFA is applied to computation for the index series.

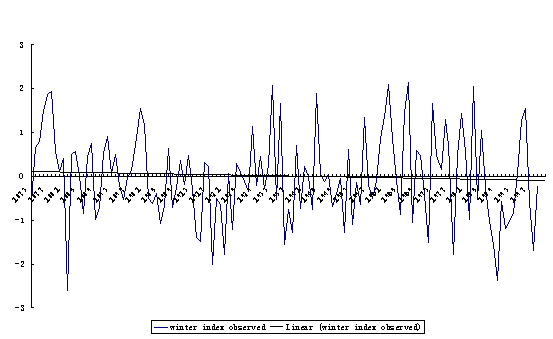
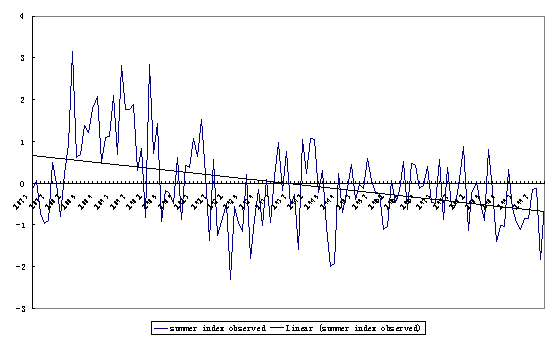
Fig.1 Yearly change in the East-Asia monsoon during 1873 to 2000 and its linear trend (upper: winter; lower: summer).

The computed results show that the East-Asian monsoon exhibits a long-term memory; it means the East-Asian monsoon has significant persistence in the yearly series. The difference between long-term memories of monsoons in winter and summer is remarkable. For the winter monsoon, α=0.55, γ=0.9（Fig.2）; but for the summer monsoon, α=0.73, γ=0.54(Fig.3), i. e. the memory of the summer monsoon is much better than that of the white noise(α=0.50).

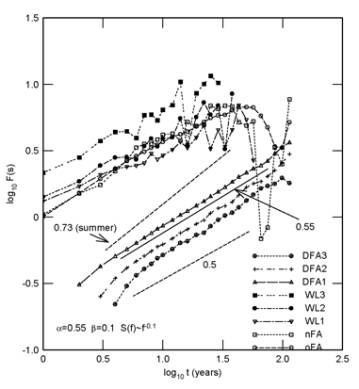
Fig.2 Log-log plots of the DFA, Wavelet and FA curves for the East-Asian monsoon in winter

DFA: detrended fluctuation analysis; DFA1: DFA with least square linear fitting, DFA2: DFA with least square quadratic polynomial fitting, DFA3: DFA with least square cubic polynomial fitting.WL1: the first derivative wavelet method, WL2: the second derivative wavelet method, WL3: the third derivative wavelet method. nFA: n steps standard fluctuation analysis, 0FA: 0 step standard fluctuation analysis.

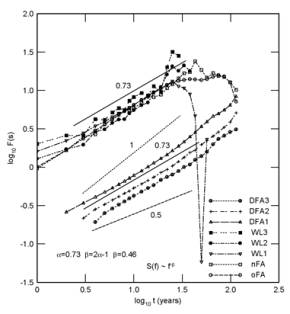Fig.3 Same as Fig.2 except for summer

It is a reasonable physical explanation for the difference between long-term memories of monsoons in winter and summer. During 1873—2000, it is just a period of global warming; the impact of the warming on the climate in winter is much stronger than that in summer, such as the warming winter around the world, the contract of ice-snow region in high-latitude. It causes the climate in winter is more variable ( Wei et al.2003), as a result, the long-term memory of monsoon in winter decreases too.

4 Concluding Remark

The weather and climate in China is extremely impacted by the East-Asian monsoon in summer; the drought/ flood in most parts of China, in particular, the wide region south of the Yellow River, are relevant to the East-Asian monsoon. The long-term memory in the climate change in the East-Asian monsoon has been found out using the DFA. The good long-term memory of the East-Asian monsoon provides a theoretical basis for its climate prediction. The better long-term memory of the summer monsoon implies a higher potential predictability.

Acknowledgements: We are indebted to the Natural Science Foundation of China for financial support: grant 40375025, the support from the Alexander von Humboldt Foundation in Bonn is appreciated. Thanks are due to Shi Neng for providing the data of the East-Asian monsoon index.

Reference

Blender R., and K. Fraedrich, 2003: Long time memory in global warming simulations, Geophysical Research Letters, 30(14), 1769, CLM7-1—7-4.

Cao H. X., 1993: Self-memorization equation in atmospheric motion. Science in China, Series B, 1993, 36(7):845–855.

Cao H. X., 2002: Self-memorization Principle of Dynamic System—Applications to Forecasting and Computing, China Geology Press, Beijing (in Chinese).

Chen L.X., Zhu Q.G, Lu H. B. et al. 1991: The East-Asian Monsoon, China Meteorological Press, Beijing (in Chinese).

Fraedrich K., 2002: Fickian diffusion and Newtonian Cooling: a concept for noise induced climate variability with long-term memory? Stochastics and Dynamics, 2(3), 403—412.

Govindan R., Vjushin D., Brenner S., Bunde A., Havlin S., Schellnhuber H.-J., 2002:Global climate models violate scaling of the observed atmospheric variability, Phys. Rev. Lett., 89, 028501.

Kantelhardt J.W., Koscielny-Bunde E., Rego H.H.A., Havlin S., Bunde A.,2001:Detecting long-range correlations with detrended fluctuation analysis, Physica A, 295, 441—454.

Koscielny-Bunde E., Bunde A., Havlin S., Goldreich Y., 1996: Analysis of daily temperature fluctuations, Physica A, 231, 393—396.

Koscielny-Bunde E., Bunde A., Havlin S., Roman H. E., Goldreich Y., Schellnhuber H.-J., 1998:

Indication of a universal persistence law governing atmospheric variability, Phys. Rev. Lett., 81, 729—732.

Kovacevic J., 1995:Wavelet and Sabbane Coding, Prentice-Hall, Englewood Cliffs, NJ.

Monetti R. A., S. Havlin, and A. Bunde, 2003: Long term persistence in the surface temperature fluctuations, Physica A320, 581—590.

Pelletier J. D., 1997:Analysis and modeling of the natural variability of climate, J. Climate, 10, 1331—1342.

Peng C.-K., Buldyrev S.V., Havlin S., Simons M., Stanley H.E., Goldberger A.L., 1994: Mosaic organization of DNA nucleotides, Phys. Rev. E, 49, 1685—1689.

Shi Neng, Zhu Qiangen, 1996: An abrupt change in the intensity of East Asia summer monsoon

  index and its relationship with  temperature  and precipitation over East China,  International J. of climatology, 17（7）,757—764.

Wei F. Y., Cao H. X., Wang L. B. 2003: Process of transition between cold and warm periods and its prediction, Acta Meteor. Sinica, 17(2), 190—204.