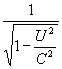文章摘要：由于牛顿力学认为加速度a＝对于所有的惯性系来讲都成立，因此牛顿力学的加速度变换式为a＝a′。这一加速度变换式使牛顿力学在理论上产生了难以克服的困难。通过数理分析和逻辑推理可以证明：加速度变换式a＝a′在理论上是不完善的。正确的加速度变换式应该为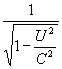：a＝ a′。

主题词：惯性系、相对论、坐标、绝对静止系、变换式、光速不变原理。

1.1.1、时间概念的内涵。

简单地讲，时间就是有起点和终点的周期性运动过程。例如，地球自转一圈为一天；地球绕太阳转公转一圈为一年。1967年以后，开始采用更加稳定的“原子钟”作为计时标准，即以铯原子133C的基态超精细结构间的微波辐射周期T作为时间单位，T与1秒之间的关系是：

1秒=9,192,631,770 T

如果在地面系中放置一个铯原子钟，并用铯原子钟来计量地面系上某一物体的运动时间，那么不论物体在地面系上运动的速度是大还是小（或是否等于光速），由于铯原子钟中原子的运动周期T，与物体运动速度V大小的变化没有任何关系，即两者在地面系中的运动都是互相独立的运动，因此铯原子钟的标准单位时间一秒钟=9,192,631,770 T，是不会随着物体运动速度的大小而发生任何变化。

1.1.2、空间概念的内涵。

容积的大小可以用三维空间坐标系（即O―XYZ）来表示。三维空间体积的大小，是根据标准单位尺长通过计算确定出来的。1961年物理学家们放弃用铂钛米尺杆作为基本长度的标准，而用氪?6的橘红光的波长λ作为长度标准。物理学家们规定，1单位米的长度等于氪?6的橘红光波长λ的165076373倍，即：

1米长度=1650763,73λ

箱子容积的大小与箱子内所存放的物体属性，以及是否放入物体是没有任何关系的。我们可以设想箱子的容积无限地扩大，这样就得到了一个与任何物质属性无关的三维空间。由于箱子容积的三维空间大小，与物体在箱子空间中运动速度的大小没有任何变化关系，即无论物体在在箱子中运动的速度是等于零还是等于光速C，箱子容积的大小是不会发生变化的。

同理，如果在地面系中放置一个标准米尺，并用该标准米尺来测量地面系上某一物体的运动距离，那么不论物体在地面系上运动的速度是大还是小（或是否等于光速），由于标准米尺的长度，与物体运动速度大小的变化没有任何关系，即两者在地面系中都是互相独立的事件，因此标准米尺的长度，不会随着物体运动速度的大小而发生任何变化。

由于地球在宇宙中是运动的，因此当火车和质点P两者沿着地球运动方向运动，并且火车地面速率V₂小于质点P地面速率V₃，即V₂＜V₃时，那么自宇宙系中观测，我们根据运动结果或运动现象就可以定性的确定出：地球的宇宙速率U₁＜火车的宇宙速率U₂＜质点P的宇宙速率U₃。

当S系与S′系两者坐标轴的方向完全相同时。假设S系与S′系两者在宇宙真空中都是惯性系，其中S系与S′系两者宇宙速率的方向相同，而S系的宇宙速率V小于S′系的宇宙速率V′，即V＜V′。

假设自S系中观测，S′系以速率U沿着正X轴线的方向运动。S系与S′系两者之间的运动虽然是相对运动，但由于S系的宇宙速率V，小于S′系的宇宙速率V′（即V＜V′），因此本文把宇宙速率较小的S惯性系，定义为“S静止系”（以下简称为S系），把宇宙速率较大的S′惯性系定义为“S′运动系” （以下简称为S′系）。

一般地讲，“静止系”和“运动系”的区别仅仅局限于两个不同的惯性系之间。虽然S惯性系与S′惯性系相比较是“静止系”，但是当S惯性系与其它惯性系相比较时，它就可能是“运动系”了。同理当S′惯性系与其它惯性系相比较时，S′惯性系也可能是“静止系”。

由于光子在宇宙真空中的速率最大，因此光子坐标系相对于所有的惯性系来讲，都是“运动系”。此外，由于宇宙坐标系在宇宙真空中的速率等于零，因此宇宙真空系相对于所有的惯性系来讲都是“静止系”。

1.3.1、人们可以使用多个惯性系，同时观测记录某一被观测事件的运动。

对于在地面系中运动的火车来讲，我们可以在三种不同的情况下，来观测火车的运动。

其一、可以单独地在S系地面系（地面系）中，观测分析被观测事件（火车）的运动即：火车速度V、运动距离X 和运动时间T。此时火车的时空坐标观测值为（X、0、0、T）。

其二、可以单独地在S′系（汽车系）中，观测分析被观测事件（火车）的运动即：火车速度V、运动距离X 和运动时间T。此时火车的时空坐标观测值为（X′、0、0、T′）。

其三、可以在S系和S′系两者中，同时观测分析被观测事件的运动即：火车在S系中的时空坐标观测值为（X、0、0、T）和火车在S′系中的时空坐标观测值为（X′、0、0、T′）。

从一个事件是否在多个惯性系中同时被观测来讲，被观测事件可以区分为： “单系事件”和 “双系事件”两种类型。

1.3.2、“单系事件”一词的定义。

假设S坐标系是惯性系。如果我们只是单独地在S系（地面系）中，观测分析物体（火车）运动时，那么我们可以把物体在S系中的运动称为：单系事件。我们自S系观测时，单系事件的坐标观测值如下图所示。

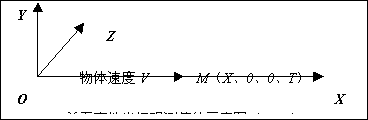
图中的M点为物体在T时刻所在的运动位置，V为物体的运动速度。由于物体（火车）在不同的时刻会具有不同的运动位置，如果物体在T时刻所在的坐标位置为（X、0、0），那么物体的时空坐标观测值为（X、0、0、T）。显然，物体在S惯性系中的时空坐标观测值（X、0、0、T）具有唯一性。

1.3.3、“双系事件” 一词的定义。

“双系事件”概念顾名思义就是从两个观测系的角度来理解和定义。假设S系和S′系都是惯性系，其中S系与S′系两者坐标轴的方向完全相同，而S′系原点O′在S系中以速率U沿着正X轴方向运动。假设在T＝T′＝0的时刻，原点O与原点O′两者重合。

如果我们自S系（地面系）和S′系（汽车系）中，同时观测物体（火车）运动，那么我们可以把同时在S系和S′系中运动的物体称为： “双系事件”。 双系事件的坐标观测值如下图所示。

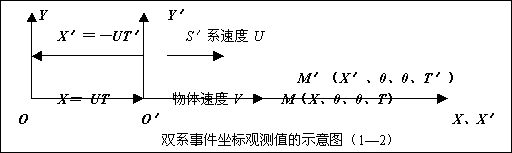
图中的M点, 为物体在T时刻所在的位置。S系坐标观测结果为M（X、0、0、T），S′系坐标观测结果为M′（X′、0、0、T′）。显然，观测值（X、0、0、T）和（X′、0、0、T′）都具有唯一性。

1.4.1、双系事件坐标变换的内涵。

对于在惯性系中观测火车的运动来讲，物理学家们可以在下面三种不同的情况下，来观测火车的运动。

其一、可以单独地在S系（地面系）中，观测分析被观测事件（即火车）的运动速度V、运动距离X 和运动时间T。此时火车的时空坐标观测值为（X、0、0、T）。

其二、可以单独地在S′系（汽车系）中，观测分析被观测事件（即火车）的运动速度、运动距离 和运动时间。此时火车的时空坐标观测值为（X′、0、0、T′）。

其三、可以在S系（地面系）和S′系（汽车系）两者中，同时观测说明火车的运动速度、运动距离 和运动时间。

火车的运动在前两种情况下，属于单系事件。而在第三种情况下，则属于双系事件。

对于第三种情况下的双系事件来讲，S系观测结果与S′系观测结果虽然不相等，但由于观测者在S系和S′系两者中，同时观测说明的事件是同一个事件（即火车运动），而事件的时空坐标又具有唯一性，因此双系事件的坐标变换是指“物体在S系中的时空坐标观测值（X、Y、Z、T），与物体在S′系中的时空坐标观测值（X′、Y′、Z′、T′）”之间的等效变换。

1.4.2、自S系观测，双系事件在S系中的时空坐标观测值为（X、0、0、T）。

对于S惯性系来讲，观测者可以单独地自S系中观测记录某一双系事件的时空坐标。假设某一双系事件在S系中，沿着正X方向做匀速运动。当时间T＝0时，双系事件与S系原点O重合。

当我们自S系观测时，双系事件在S系中的运动距离为X，运动时间为T。于是自S系观测，双系事件在S系中的时空坐标观测值为（X、0、0、T）。而双系事件在S系中的速率V为：

V＝ （1―1）

当双系事件为光子运动，而S系为宇宙真空系时。如果光子在宇宙真空系中的运动距离为X，运动时间为T，那么上式中的速率V等于自宇宙真空系观测，光子在宇宙真空系中的速率C即： C＝

1.4.3、自S′系观测，双系事件在S′系中的时空坐标观测值为（X′、0、0、T′）。

对于S′惯性系来讲，观测者可以单独地自S′系中观测记录某一双系事件的时空坐标。假设某一双系事件在S′系中，沿着正X′方向做匀速运动。当时间T′＝0时，双系事件与S′系原点O′重合。

当我们自S′系观测时，双系事件在S′系中的运动距离为X′ ，运动时间为T′。于是自S′系观测，双系事件在S′系中的时空坐标观测值为（X′、0、0、T′）。而双系事件在S′系中的速率V′为：

V′＝ （1―2）

当双系事件为光子时，那么上式中的速率V′等于自S′系观测，光子在S′系中的运动速率C′即：

C′＝

1.4.4、自S系观测， S′系原点O′中的时空坐标观测值为（UT、0、0、T）。

假设S′系在S系中以速度U沿着正X方向运动，而双系事件在S系中以速度V沿着正X方向做匀速运动。对于（X―UT）关系式来讲，它在理论上所具有的物理含意是什么？很多人对此可能是不清楚的，我们不妨分析说明一下这个问题。

自S系观测时，人们通常只把观测值（X、0、0、T）看成是，运动物体在S系中的观测坐标，却很少有人主动地把坐标观测值（UT、0、0、T）看成是：原点O′在S系中的观测坐标。

如果我们把坐标观测值（X、0、0、T）与（UT、0、0、T），两个时空坐标中的运动距离相减后，就会得到双系事件与原点O′两者，在S系中的运动距离之差X_―UT即：

X_―UT＝X ―UT

从理论上讲，运动距离之差（X ―UT），与双系事件在S′系中的运动距离X′相对应，即距离之差（X ―UT）是自S系观测时，物体从S′系原点O′运动到M点的距离。

应该指出的是：运动距离X′是自S′系观测得到的，而运动距离之差（X ―UT）则是用S系观测值计算出来的。从这一点来讲，运动距离之差（X ―UT）事实上是自S系观测到的“双系事件在S′系中的运动距离”。

由于双系事件和S′系原点O′两者在S系中的运动时间都等于时间T，因此自S系观测, 双系事件在S系中的时空坐标观测值应该为（X_―UT、0、0、T）。于是自S系观测，双系事件在S′系中的速率V_―UT为：

V_―UT＝＝＝V―U （1―3）

由上式可知，当双系事件为光子时，那么自S系观测，光子在S′系中速率V_―UT等于自S系观测，光子与物体两者在S系中的速率之差。

1.4.5、自S′系观测， S系原点O的时空坐标观测值为（―UT′、0、0、T′）。

同样，对于（X′+ UT′）关系式来讲，它在理论上所具有的物理含意是什么？很多人对此也是不清楚的，我们不妨分析说明一下这个问题。

自S′系观测时，人们通常只把坐标观测值（X′、0、0、T′）看成是，运动物体在S′系中的观测坐标，很少有人把坐标观测值（―UT′、0、0、T′）看成是，原点O在S′系中的观测坐标。

如果我们把坐标观测值（X′、0、0、T′）与（―UT′、0、0、T′），两个时空坐标中的运动距离相减，那么得双系事件与原点O两者，在S系中的运动距离之和X_S′即：

X_S′＝X′+ UT′

从理论上讲，运动距离之和（X′+ UT′），与双系事件在在S系中的运动距离X相对应，即距离之和（X′+ UT′）是自S′系观测时，物体从S系原点O运动到M点的距离。

应该指出的是：运动距离X是自S系观测到的，而运动距离之和（X′+ UT′）则是用S′系观测值计算出来的。从这一点来讲，运动距离之和（X′+ UT′）事实上是自S′系观测到的“双系事件在S系中的运动距离”。

由于双系事件和S系原点O两者在S′系中的运动时间都等于时间T′，因此自S′系观测, 双系事件在S′系中的时空坐标观测值应该为（X_S′、0、0、T′）。于是自S′系观测，双系事件在S系中的速率V′为：

V _S′＝＝＝V′+ U （1―4）

由上式可知，当双系事件为光子时，那么自S′系观测，光子在S系中速率V _S′等于自S′系观测，光子与物体两者在S′系中的速率之和即：

C _S′＝＝V′+ U

假设S系是静止系，而 S′系是运动系，其中S系与S′系两者坐标轴的方向完全相同，设S′系原点O′在S系中，以速率U沿着正X 轴方向运动，而质点P在S系中，以速率V沿着正X 轴方向运动。

假设自T＝T′＝0的时刻起，S系原点O，S′系原点O′与质点P这三者重合。当质点P沿着X轴运动到空间某一点M后。对于质点P所在位置来讲。

自S系中观测，质点P的时空坐标观测值为M（X、0、0、T），而自S′ 运动系中观测，质点P的时空坐标观测值为M′（X′、0、0、T′）。此时M（X 、0、0、T）坐标点与M′（X′、0、0、T′）坐标点，两者是空间中的同一M点。如下图所示。

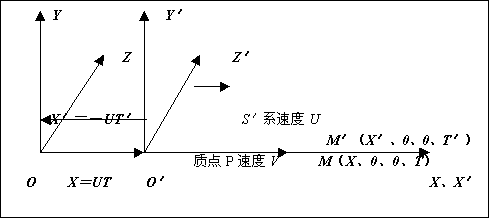
上图中的M点，为质点P运动了T时刻后所到达的位置。需要指出的是：时空坐标观测值M（X、0、0、T）和M′（X′、0、0、T′）在理论上应该具有两方面的含义。

其一、距离X与X′分别是S系和S′系中的三维空间长度。而时间T和T′分别是自T＝T′＝0的时刻开始计量，在S系和S′系中已经自然流逝，或实际发生过的时间间隔。此时时空坐标（X、0、0、T）和（X′、0、0、T′）与任何物体的运动无关。

其二、距离X与X′两者分别是：自T＝T′＝0的时刻起，双系事件（即质点P）在S系和S′系中的运动距离。而时间T和T′两者分别是：自T＝T′＝0的时刻起，双系事件（即质点P）在S系和S′系中的运动时间。此时时空坐标（X、0、0、T）和（X′、0、0、T′）与物体的运动相关。

由于本文分析研究的坐标变换问题是：物体在两个不同惯性系中的坐标进行等效变换的问题，因此时空坐标点（X、0、0、T）与（X′、0、0、T′），两者到原点O和O′的长度和时间，应该指的是第二种含义。

即坐标观测值（X、T）是指双系事件（即光子或质点P），在S系中从原点O运动到空间M点后，实际发生的运动距离和运动时间。而坐标观测值（X′、T′）是指双系事件在S′系中，从原点O′运动到空间M点后，实际发生的运动距离和运动时间。两者所指的对象不是与运动无关的宇宙空间和自然流逝的时间。

由上述分析可以确定：（X、0、0、T）坐标点和（X′、0、0、T′）坐标点，本质上是物体运动的坐标点。其中距离X和X′两者本质上是物体的运动距离，而时间T和T′两者本质上是物体的运动时间。

对于不同的惯性系来讲，由于S′系在S系中的速率U会发生变化，因此S′系的速率U在坐标变换式中是一个变量。

同理，对于不同的观测事件来讲，由于双系事件（光子或质点P的运动），在S系中的速率V，或在S′系中的速率V′，也会发生变化，因此双系事件的速率V（或V′），在坐标变换式中也是一个变量。

由于坐标变换式的分析推证过程，涉及U和V（或V′）两个速率变量，因此坐标变换式中包含着速率U和V（或V′）两个运动变量。

我们自S系和S′系中，观测同一个事件时，可以得到两组不同的时空坐标观测值。而坐标变换式的本质是：能把这两组不同的时空坐标观测值进行等效的变换。即利用坐标变换式可以把S系的时空坐标观测值（X、Y、Z、T），等效的变换成S′系的时空坐标观测值（X′、Y′、Z′、T′）。

双系事件质点P在S系中的坐标X，具有两种不同性质的含义。

其一、坐标X是指质点P到S系原点O的几何空间长度，此时坐标X不属于质点P运动变量的范围。

其二、如果双系事件质点P在S系中具有速率V，那么坐标X是指质点P在S系中的运动距离即X＝V T，此时坐标X属于质点P运动变量的范围。

2.3.1、S系与S′系两者时空坐标变换的线性方程式。

由于双系事件（即光子或质点P）的S系（X、0、0、T）坐标点，与S′系（X′、0、0、T′）点，两者是同一个空间M点，并且两者在数值上都具有唯一性，因此两坐标点之间的数值变换关系必定是一种线性比例关系。

如果把坐标观测值（X′、T′）看成自变量、把坐标观测值（X、T）看成因变量，那么自变量（X′、T′）与因变量（X、T），之间的线性变换关系，可以表示为下面的数学形式。

X＝AX′+ BT′+ C (2―1)

T＝DX′+ ET′+ F

上式中的A、B、C、D、E、F是六个待定系数常量。我们可以利用一些特殊的时空坐标点，来分析确定这六个未知的系数常量。

反之，如果把坐标观测值（X、T）看成自变量、把坐标观测值（X′、T′）看成因变量，那么自变量（X、T）与因变量（X′、T′），之间的线性变换关系，可以表示为下面的数学形式。

X′＝A′X + B′T + C′ (2―2)

T′＝D′X + E′T + F′

上式中的A′、B′、C′、D′、E′、F′也是六个待定系数常量。我们可以利用一些特殊的时空坐标点，来分析确定这六个未知的系数常量。

应该指出的是：由于（X、0、0、T）坐标点与（X′、0、0、T′）坐标点，两者是同一个空间M点，并且两者在数值上都具有唯一性，因此（2―1） 方程式中的坐标变量（X、T、X′、T′），与（2―2）方程式中的坐标变量（X、T、X′、T′）在数值上应该是完全相等的。从这一点来讲，（2―1）和（2―2）两式实质上是同一个方程式。

2.3.2、利用特殊时空坐标点求解出的运动距离变换式。

在T＝T′＝0时刻。由于原点O、原点O′以及质点P（即双系事件）这三者重合，因此自S系观测，质点P的运动距离X＝0，运动时间T＝0。同样，自S′系中观测，质点P的运动距离X′＝0，运动时间T′＝0。

把X＝X′＝0、T＝T′＝0特殊点，代入（2―1）式后可以得到：C＝0，F＝0。于是（2―1）式可化简为：

X＝AX′+ BT′ （2―3）

T＝DX′+ ET′

上面两式就是S系与S′系两者之间运动坐标的线性变换式。

把X＝X′＝0、T＝T′＝0特殊点，代入（2―2）式后可以得到：C′＝0，F′＝0。于是（2―2）式可化简为：

X′＝A′X + B′T （2―4）

T′＝D′X + E′T

应当指出的是：当S′系在S系中的运动速度U≠0时，由于变量X′与X、变量T′与T的数值不相等，即X′≠X、T≠T′，因此（2―3） 线性方程组中的A、B、D、E这四个系数常量，与（2―4）线性方程组中的A′、B′、D′、E′这四个系数常量，其数值是不相等的。即A≠A′、B≠B′、D≠D′、E≠E′。

只有当S′系速度U＝0时，那么由于S系与S′系两者是同一个惯性系，而变量X′与X数值相等、变量T′与T的数值相等，因此系数常量A＝A′＝1、B＝B′＝0、D＝D′＝0、E＝E′＝1。

2.3.3、本文推导距离变换式X＝A（X′+ U T′） 的过程如下。

当质点P（即双系事件）在S系中的速率V＝0，并且质点P与S系原点O重合时。自S系中观测，质点P在S系中的坐标X＝0。把该特殊点代入（2―3）后，可以得到下面的关系式：

X＝AX′+ BT′＝0。

此时，对于质点P在S′系中的运动来讲，由于S系与S′系两者之间的运动是相对运动，因此质点P在S′系中的速率等于―U。

于是自S′系观测，质点P在S′系运动距离X′和运动时间T′满足下面的关系式：

―U＝＝― （2―5）

把上式代入（2―3）后得下面的关系式：

X＝A（X′+ U T′） （2―6）

由于上式中的观测值X是质点P在S系中的运动距离，观测值X′是质点P在S′系中的运动距离。而式中的观测值U T′是自S′系观测时，原点O在S′系中的运动距离，因此（2―6）式本质上是物体运动距离的变换式。

对于质点P在S系中的运动距离来讲：自S系观测，质点P在S系中的运动距离为X 。自S′系观测，质点P在S系中的运动距离为（X′+ UT′）。显然（2―6）式中的系数A是把距离（X′+ U T′），变换成距离X的变换系数。

根据（2―6）式可以得到下面的关系式：

X＝ X′+ U T′ （2―7）

上式中的还原系数与变换系数A恰恰相反，它是把观测距离X ，还原成观测距离( X′+ UT′)的变换系数。此时我们绝对不能用变换系数A，把距离X还原成 ( X′+ U T′)，因为这样还原的方法，不符合数学运算法则要求。

从数学运算法则上讲，当变换系数A＝1时，A＝关系式是正确的。然而在A≠1的情况下，由于A≠，因此如果有人认为A＝此时仍然成立，那么这种看法显然是错误的。

2.3.4、本文分析推导距离变换式X′＝A′（X―U T）的过程如下。

当双系事件质点P在S系中的速率V＝U，并且质点P与S′系原点O′重合时。自S′系观测，质点P在S′系中的坐标X′＝0。把该特殊点代入（2―4）后，可以得到下面的关系式：

X′＝A′X + B′T＝0。

此时，对于质点P在S系中的运动来讲，由于S系与S′系两者是相对运动，因此质点P在S系中的速率等于U。

于是自S系观测，质点P在S系运动距离X和运动时间T满足下面的关系式：

U＝＝― （2―8）

把上式代入（2―4）后得下面的关系式：

X′＝A′（X―U T） （2―9）

由于上式中的X′是质点P在S′系中的运动距离，X是质点P在S系中的运动距离。而式中的UT是自S系观测时，原点O′在S系中的运动距离，因此（2―9）式本质上是物体运动距离的变换式。

对于质点P在S′系中的运动距离来讲：自S′系观测，质点P在S′系中的运动距离为X′ 。自S系观测，质点P在S′系中的运动距离为（X―U T）。显然（2―9）式中的系数A′是把距离（X―U T），变换成距离X′的变换系数。

根据（2―9）式可以得到下面的关系式：

X′＝X―U T （2―10）

上式中的系数与变换系数A′恰恰相反，它是把运动距离X′，还原成运动距离（X―U T）的变换系数。此时我们不能用变换系数A′，把距离X′还原成（X―U T），因为这样的还原方法，也不符合数学运算法则要求。

从数学运算法则上讲，当变换系数A′＝1时，A′＝关系式是正确的。然而在A′≠1的情况下，由于A′≠，因此如果有人认为A′＝此时成立，那么这种看法显然是错误的。

--3--